隠れフリーザ様親衛隊のハナオです。
今回の目で見て耳で聴く音楽理論は、Section1「 楽譜を音符を学ぼう 」の第5回「 音符の長さ 」( 後編 )です。
「 単純音符 」と「 付点音符 」
「 単純音符 」
まずはおさらいから。
前回の記事でもアップした、「 全音符 」から「 十六分音符 」までを1小節ごとに並べた譜面です。

これらの音符には「 単純音符 」という総称があります。
「 付点音符 」
では、「 単純 」では無い方? の音符の説明に入ります。
下の画像をご覧ください。

「 四分音符 」の「 符頭 」の右に小さな点が付いています。
点は描き間違いでも汚れでもありません。
この点が付くと、音符の長さが元の音符の1.5倍になります。
つまり画像の音符は「 四分音符 」+「 八分音符 」分の長さを持つことになります。
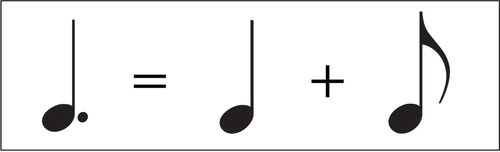
この音符の名称を「 付点四分音符 」と言います。
同様に「 付点 」が付くと、すべての音符は長さが1.5倍になります。

上記を総称して「 付点音符 」と呼びます。
「 複付点音符 」

今度は「 付点 」が2つ付きました。
音符の長さは1つめの「 付点 」の更に半分の長さが加算されます。
つまり、「 四分音符 」+「 八分音符 」+「 十六分音符 」がこの音符の長さになります。

この音符は「 複付点四分音符 」と呼び、端的に言うと「 四分音符 」の1.75倍の長さになります。
こちらも「 付点音符 」同様に、すべての音符に点2個がくっついて1.75倍の長さへと変わります。

上記を総称して「 複付点音符 」と呼びます。
「 付点音符 」捕捉
「 付点 」は3つ以上付くこともあり、その場合(前の音符の0.5倍の長さが付加される法則)が適用されます。
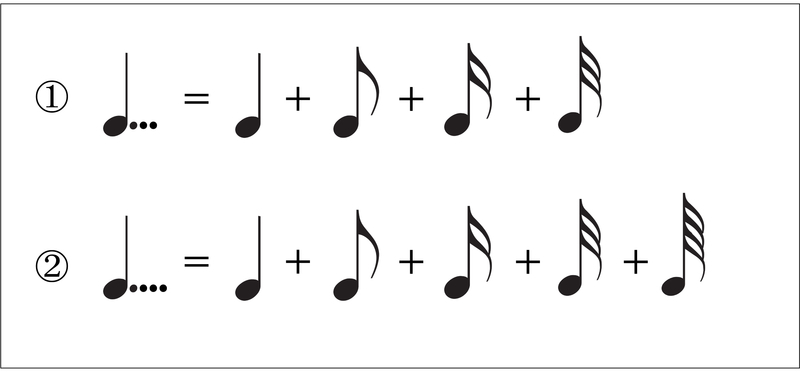
①を「 複々付点四分音符 」、②を「 複々々付点四分音符 」といいます。
これらはごく稀にクラシック音楽の譜面で見られます。
「 タイ 」と「 スラー 」
下の譜面をご覧ください。

わざと「 付点音符 」を多めに使ってみましたが、なんか読み辛くありません?
前回の記事で取り上げた「 連桁 」を用いていないせいもありますが、拍の表裏を見失いそうになりますね。
ハナオは自分で楽譜を書く場合、「 付点音符 」の使用は極力避けます。
演奏者が見易いよう拍ごとに「 連桁 」でまとめ、「 付点 」に相当する音符は「 タイ 」で繋ぎます。

「 タイ 」は同じ高さの音を続けて伸ばすことを指示する記号です。
例えば、「 四分音符 」と「 八分音符 」を「 タイ 」で繋げると、音の長さが「 付点四分音符 」と一緒になります。

さきほどの譜面を「 タイ 」と「 連桁 」を用いて書き直すと下のようになります。

いかがでしょう、ちょっとゴチャゴチャしてますかね~。
どちらが読み易いかは慣れやフレーズによりますが、音のブログでは基本「 付点音符 」を避け「 タイ 」中心に記譜してまいります。
ご了承ください。
「 タイ 」と似た表記の音楽記号に「 スラー 」があります。

異なった高さの2つ以上の音を滑らかに繋げて演奏する指示記号ですが、本来「 タイ 」と「 スラー 」は別の技法を求めているわけで、一緒に覚えるべきではないと思っています。
学校の音楽の授業にてサラッと流す程度でまとめて教しえられてしまうがゆえ、「 タイ 」と「 スラー 」をごちゃ混ぜにして覚えている人が大勢います。
少々乱暴な物言いですが、繊細なタッチで曲調がガラリと変わってしまうクラシックは別として、ロックやポップスのバンドスコアを読む分には「 タイ 」だけ意識していれば充分です。
「 スラー 」は弦楽器の「 ハンマリング・オン 」「 プリング・オフ 」「 タッピング 」くらいでしか表記を必要としません。
「 ハンマリングなんちゃら 」以下の用語は、また別の記事にてご説明いたします。
なお、「 タイ 」と「 スラー 」で音と音を繋いでいる横向きの三日月みたいな線は「 弧線 」と呼びます。
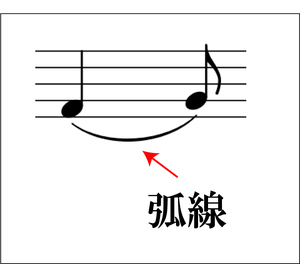
楽譜上で「 弧線 」を用いた表記は他にもありますが、それらは別項にて取り上げます。
「 連符 」
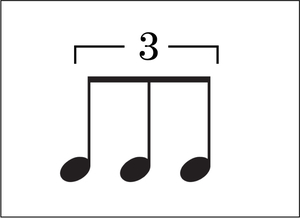
また意味不明な音符が出てきましたね~。
「 符尾 」の上に「 3 」とか書いてあるし、なんじゃこりゃ?
いきなりですが皆さんに質問です。
1÷3はいくつですか?

はい、シンキングタ~~イム!!
……なんかいりませんね、答えは「 0.3333…… 」です。
整数では割り切れません。
1つの音価を3等分の長さで演奏する場合には「 3連表記 」を用い、出来上がった音符のまとまりはその名もズバリ「 三連符 」といいます。
例えば「 四分音符 」の「 3連表記 」には、半分( = 2等分 )の長さの「 八分音符 」を3つ並べて「 3 」でくくれば「 三連符 」の出来上がりです。
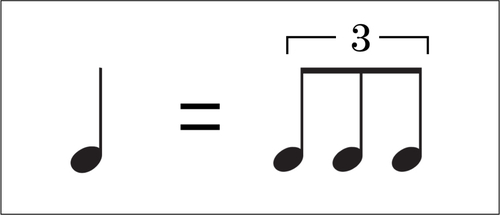
この「 一拍三連 」が基本リズムになっている曲や歌は多くあり、皆さんも耳に覚えがあるはずです。
下記に日本のヒットソングからいくつかピックアップしてみましたので参考にしてください。
ビリーバンバン「 白いブランコ 」
グレープ「 精霊流し 」
竹内まりあ「 リンダ 」
小坂恭子「 想い出まくら 」
プリンセスプリンセス「 M 」
井上陽水奥田民生「 ありがとう 」
松田聖子「 SWEET MEMORIES 」
中島みゆき「 時代 」
加山雄三「 君といつまでも 」
山下久美子「 バスルームより愛をこめて 」
なお、今回は詳しく取り上げませんが、スイングやシャッフルなどの“ハネる”ビートも「 一拍三連 」にカテゴライズされます。
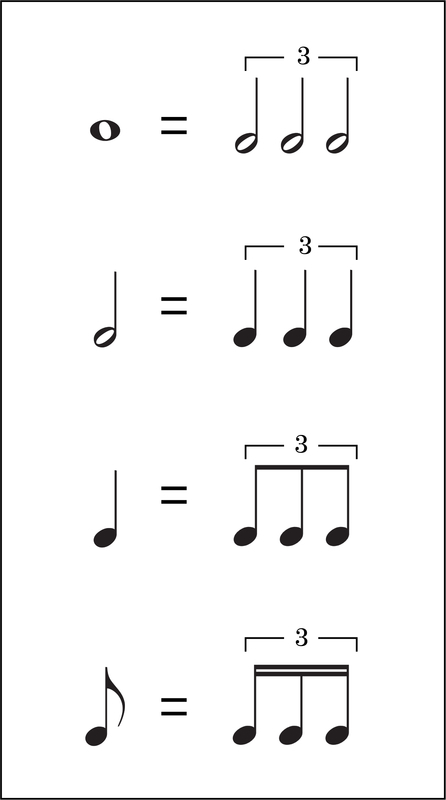
「 四分音符 」以外の音符も「 三連符 」にすることができます。
各音符を「 3等分 」したときの「 連符 」は下のとおりです。
「 三連符 」は見ただけでは感覚がつかみ難いと思われますので、音声データも載せておきます。

「 連符 」は「 3等分 」に限らず、「 5等分 」「 6等分 」「 7等分 」「 9等分 」「 10等分 」「 11等分 」……など、理論上「 2 」と「 4 」の公倍数以外の等分はいくらでも作れます。

さきほどの「 複々付点音符 」と違い、すさまじい数の「 連符 」の方はクラシック音楽やロック系ミュージックなどの速弾きフレーズとしてガンガン登場してきます。
演奏テクニックをひけらかすためにも(笑)、しっかり覚えておいてください。
次回の、目で見て耳で聞く音楽理論は、「 休符はしっかり弾きましょう 」です。
最後までお読みいただきありがとうございました。